hdg-wireless | glossary

[befindet sich noch im Aufbau... kann und wird 'noch' Fehler und Fehlfunktionen enthalten! Start 07.2023, Stand: 12.2025]

Der Freiraumdämpfungsfaktor D_F beschreibt die Dämpfung D der Leistung P einer elektromagnetischen Welle im freien Raum in Abhängigkeit von der Frequenz f (bzw. Wellenlänge λ) und dem Abstand d zwischen der Sende- und Empfangsantenne.

Freiraumdämpfungsfaktor D_F:

D_F = Freiraumdämpfungsfaktor [1]
P_S[tx] = Strahlungsleistung (Sendeantenne) [W]
P_S[rx] = Strahlungsleistung (Empfangsantenne) [W]
π = Kreiszahl (Pi) [1]
r = Radius [m]
λ = Wellenlänge [m]
A_◕ = Kugelfläche (Strahlungsdivergenz) [m²]
A_W = Antennenwirkfläche [m²]
f = Frequenz [Hz]
c₀ = Lichtgeschwindigkeit im freien Raum [ms^-1]

Die Freiraumdämpfung F eines Isotropstrahlers beschreibt die Abnahme der Strahlungsleistungsdichte S einer sich kugelförmig ausbreitenden elektromagnetischen Welle in Abhängingkeit vom Abstand d (Radius r) der Kugeloberfläche A_◕ (Position: Empfangsantenne) zur Kugelmitte (Position: Sendeantenne).

Daraus läßt sich die theoretisch maximale Strahlungsleistung P_S(max) ermitteln, die an der gedachten Kugeloberfläche A_◕ von einer Antenne empfangen werden kann.

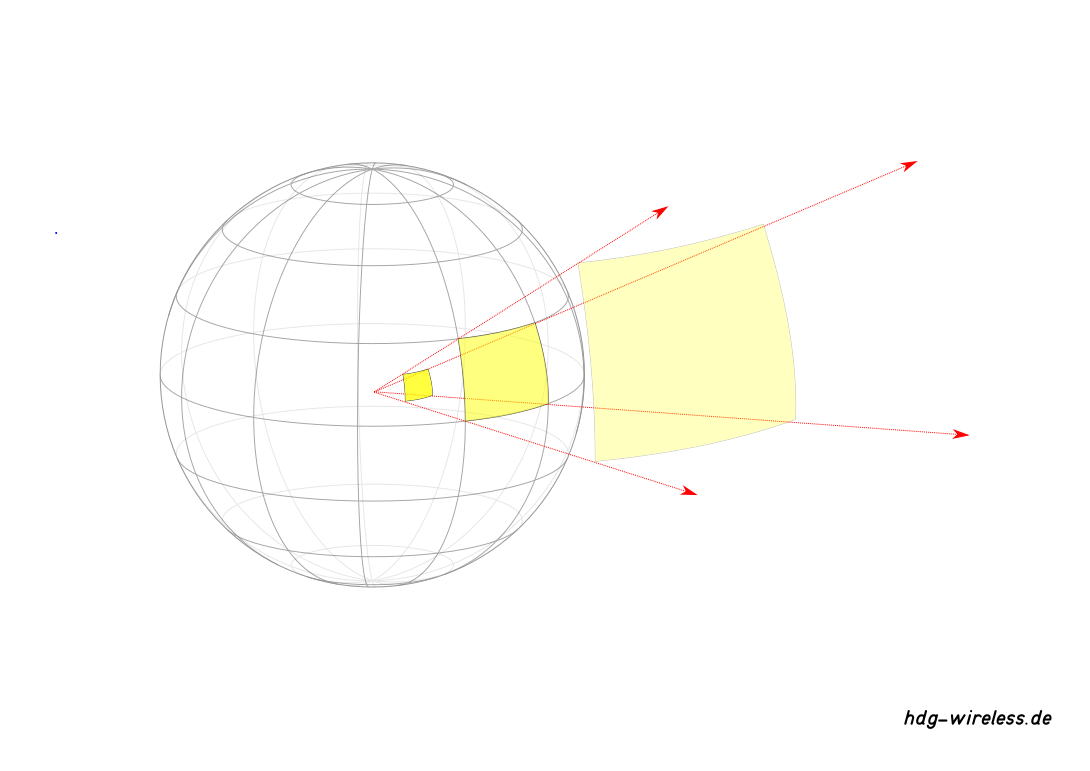
Ursächlich für die Freiraumdämpfung F ist die Abnahme der Strahlungsleistungsdichte S als Folge der Strahlungsdivergenz, also der gleichmäßigen Signalausbreitung in alle Richtungen.

Freiraumdämpfungsfaktor D_{F[Leistung P]}:

D_F = Freiraumdämpfungsfaktor [1]
P_S[tx] = Strahlungsleistung (Sendeantenne) [W]
P_S[rx] = Strahlungsleistung (Empfangsantenne) [W]

Der Freiraumdämpfungsfaktor D_F läßt sich aus dem Verhältnis zur ausgesendeten Strahlungsleistung (Sendeantenne) P_S[tx] zur Strahlungsleistung (Empfangsantenne) P_S[rx] an der Empfangsantenne ermitteln.

Freiraumdämpfungsfaktor D_{F[Wellenlänge λ]}:

F = Freiraumdämpfung [1]
π = Kreiszahl (Pi) [1]
r = Radius [m]
λ = Wellenlänge [m]

Der Freiraumdämpfungsfaktor D_F läßt sich aus dem Radius r (Abstand d zwischen Sende- und Empfangsantenne) und der Wellenlänge λ der betrachteten elektromagnetischen Welle errechnen.

Freiraumdämpfungsfaktor D_{F[Kugelfläche A◕]}:

D_F = Freiraumdämpfungsfaktor [1]
A_◕ = Kugelfläche [m²]
A_W = Antennenwirkfläche [m²]

Der Freiraumdämpfungsfaktor D_F läßt sich aus dem Verhältnis der theoretischen Kugeloberfläche A_◕ der sich in alle Richtungen ausbreitenden elektromagnetischen Welle im Abstand zur Sende-/Empfangsantenne und der Antennenwirkfläche A_W der Empfangsantenne errechnen.

Freiraumdämpfungsfaktor D_{F[Frequenz f]}:

D_F = Freiraumdämpfungsfaktor [1]
π = Kreiszahl (Pi) [1]
r = Radius [m]
f = Frequenz [Hz]
c₀ = Lichtgeschwindigkeit im freien Raum [ms^-1]

Der Freiraumdämpfungsfaktor D_F läßt sich aus dem Radius r (Abstand d zwischen Sende- und Empfangsantenne) und der Frequenz f der betrachteten elektromagnetischen Welle errechnen.

Für die Berechnung der Freiraumdämpfung F wird einerseits die Kugelfläche A_◕ benötigt:

A_◕ = Kugelfläche [m²]
π = Kreiszahl (Pi) [1]
r = Radius [m]

Und andererseits die theoretische Antennenwirkfläche A_W0 einer Isotropantenne als Empfangsantenne.

A_W0 = Antennenwirkfläche (Isotropantenne) [m²]
λ = Wellenlänge [m]
π = Kreiszahl (Pi) [1]

Das Verhältnis der beiden Flächen ergibt dann den Freiraumdämpfungsfaktor D_F.

D_F = Freiraumdämpfungsfaktor [1]
A_◕ = Kugelfläche [m²]
A_W = Antennenwirkfläche [m²]

Bei bekannter Strahlungsleistungsdichte S entnimmt die theoretische Antennenwirkfläche (Isotropantenne) A_W0 aus einer ebenen^[1] Wellenfront Energie E.

Die Antennenwirkfläche A_W einer Empfangsantenne ist frequenzabhängig.
Die Frequenzabhängigkeit der Antennenwirkfläche A_W ist darin begründet, dass eine Antenne kein geometrischer Punkt sein darf, da die rein theoretische, punktförmige Antenne (Isotropstrahler ≙ Punktstrahler) keine Leistung P aufnehmen kann, da an einem Punkt keine Spannung U möglich ist.
Eine Antennenwirkfläche A_W sollte also in den Mindestausdehnungen von der Größe der Wellenlänge λ aufweisen.

Nach der Abstrahlung der elektromagnetischen Welle an der Sendeantenne bleibt die Wellenlänge λ unverändert und der Freiraumdämpfungsfaktor D_F verhält sich proportional zum Quadrat des Radius r (Entfernung).

F = Freiraumdämpfung [1]
π = Kreiszahl (Pi) [1]
r = Radius [m]
λ = Wellenlänge [m]

^[1] Eine Kugeloberfläche ist natürlich keine ebene Fläche. Bei verhältnismäßig großen Entfernung kann aber ein kleiner Ausschnitt der Oberfläche als eine Ebene betrachtet werden und somit auch der Ausschnitt einer elektromagnetischen Welle der auf die verhältnismäßig kleine Wirkfläche einer Empfangsantenne auftrifft als ebene Wellenfront.

⇒ Antennenwirkfläche
⇒ Dämpfung
⇒ Freiraumdämpfung
⇒ Frequenz
⇒ Isotropstrahler [ ⇒Isotropantenne ]
⇒ Kreiszahl
⇒ Leistung
⇒ Lichtgeschwindigkeit
Radius
⇒ Strahlungsdivergenz
⇒ Strahlungsleistung
⇒ Strahlungsleistung [ ⇒Erp ]
⇒ Strahlungsleistungsdichte
⇒ Wellenlänge