hdg-wireless | glossary

[befindet sich noch im Aufbau... kann und wird 'noch' Fehler und Fehlfunktionen enthalten! Start 07.2023, Stand: 12.2025]

Die Leistungsanpassung R_i = R_a ist eine Widerstandsanpassung, bei der Quellwiderstand R_i und Lastwiderstand R_a den gleichen Wert haben.

Leistungsanpassung: R_i = R_a       [Z_i = Z_a]

Dabei handelt es sich um eine elektrische Anpassungsschaltung, die einen maximalen Wirkungsgrad η erzielen soll.

Leistungsanpassung: R_i = R_a       [Z_i = Z_a]

η = Wirkungsgrad [1]
P = Leistung (Last) [W]
P₀ = Bezugsleistung (Quelle) [W]
R_a = Lastwiderstand [Ω]
R_i = Quellwiderstand [Ω]

Leistungsanpassung:

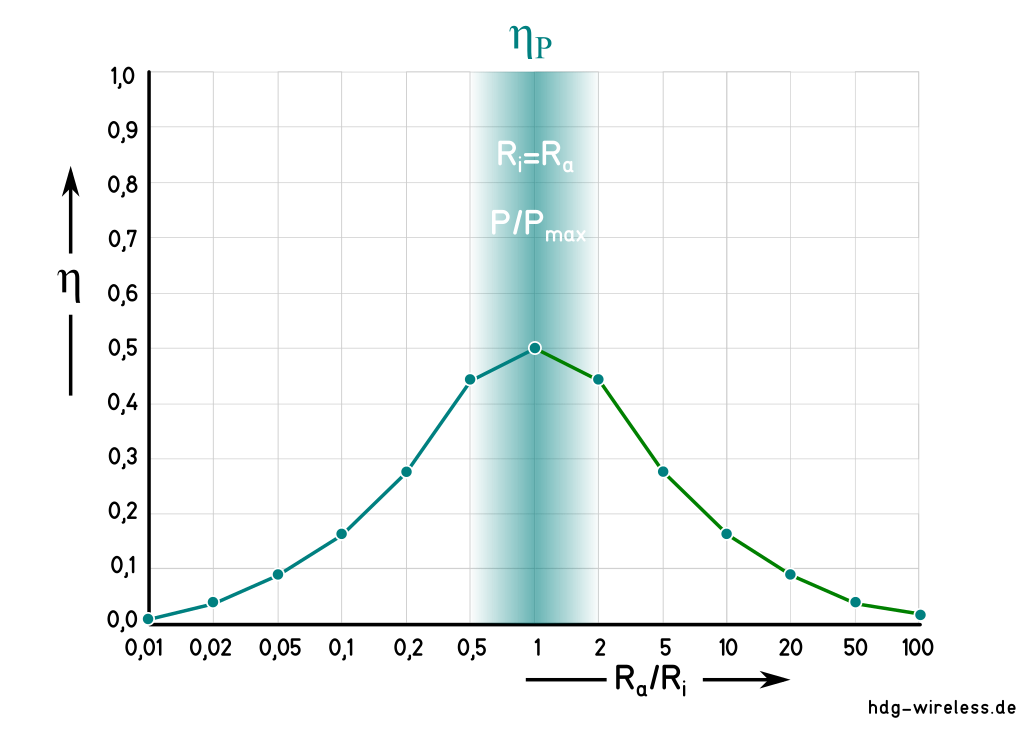
η = Wirkungsgrad [1]
P = Leistung [W]
R_i = Quellwiderstand [Ω]
R_a = Lastwiderstand [Ω]

Die Leistungsanpassung R_i = R_a soll die maximal verfügbare Leistung P der Quelle (z.B. Antenne) möglichst vollständig an die Last (z.B. Empfänger) weitergeben.
Das ist der Fall, wenn der Innenwiderstand R_i der Quelle den gleichen Wert aufweist wie der Außenwiderstand R_a der Last.

Diese Form der Anpassung findet Verwendung bei Quellen mit geringer elektrischer Leistungsabgabe. Da die Hälfte der Leistung P am Innenwiderstand R_i der Quelle in Wärme umgewandelt wird, sind hohe Leistungen hier nicht von Vorteil.

Ableitung: Leistungsanpassung R_i = R_a

Die beiden "Extremfälle" einer elektrischen Schaltung sind der offene Stromkreis (≙ Leerlauf; R_a = ∞, d.h. U = U_L = U₀ und I = 0) und der Kurzschluß (R_a = 0, d.h. U = 0 und I = max.).

Beide Schaltungen führen zu dem gleichen Ergebnis, dass am Lastwiderstand R_a (Verbraucher) keine Leistung P abgegeben werden kann, d.h. sie ist gleich Null:

P = UI = 0     (für U = 0 oder I = 0 )

P = Leistung [W]
U = Spannung [V]
I = Strom [A]

Unter Berücksichtigung des ohmschen Gesetzes [ U = RI ] gilt Folgendes:

Kurzschluss (U = 0, d.h. I = max.):
Die Schaltung ist ″kurzgeschlossen″, d.h. der Stromkreis ist zwar geschlossen, aber es ist kein Lastwiderstand R_a (Verbraucher) enthalten. Dadurch ist der Außenwiderstand R_a theoretisch gleich 0 und der Stromfluß maximal.

U₀ = Quellenspannung [V]
I₀ = Stromquelle [A]
U_i = Spannungsabfall am Innenwiderstand [V]
U_a = Spannungsabfall am Außenwiderstand [V]
I_i = Stromfluß durch den Innenwiderstand [A]
I_a = Stromfluss durch den Außenwiderstand [A]
R_i = Innenwiderstand [Ω]
R_a = Außenwiderstand [Ω]

Der Strom I wird maximal und die Spannungsquelle U₀ wird nur noch durch den Innenwiderstand R_i begrenzt.

Offener Stromkreis (I = 0, d.h. U = ∞):
Ist die Schaltung offen, d.h. der Stromkreis ist nicht geschlossen, dann fließt kein Strom I und der Außenwiderstand R_a ist theoretisch unendlich groß.

U₀ = Quellenspannung [V]
U_i = Spannungsabfall am Innenwiderstand [V]
U_a = Spannungsabfall am Außenwiderstand [V]
I_i = Stromfluß durch den Innenwiderstand [A]
I_a = Stromfluss durch den Außenwiderstand [A]
R_i = Innenwiderstand [Ω]
R_a = Außenwiderstand [Ω]

An den Klemmen wird die Leerlaufspannung U_L maximal und nimmt den Wert der Quellenspannung U₀ an.

Die Leistung P_a(max) an der Last wird maximal, wenn die beiden Werte für Strom I_max und Spannung U_max halbiert werden:

Für P_a gilt:

Für P_a(max) (R_i = R_a) gilt:

P = Leistung [W]
U₀ = Quellenspannung [V]
U = Spannung [V]
I = Strom [A]
R_i = Innenwiderstand [Ω]

Bei Lastanpassung (Quellwiderstand R_i = Lastwiderstand R_a) nimmt der Außenwiderstand R_a dieselbe Leistung P auf wie der Innenwiderstand R_i der Quelle und die Leistungsausbeute (Leistung P_max) wird maximal.

Der Wirkungsgrad η ist bei Leistungsanpassung (R_i = R_a) gleich 1, also 100 %.

Wirkungsgrad: Leistungsanpassung

Die Leistung P_a(max) an der Last wird maximal, wenn die beiden Werte für Strom I_max und Spannung U_max halbiert werden:

Für P_a gilt:

Für P_a(max) (R_i = R_a) gilt:

P = Leistung [W]
U₀ = Quellenspannung [V]
U = Spannung [V]
I = Strom [A]
R_i = Innenwiderstand [Ω]

Anpassung:

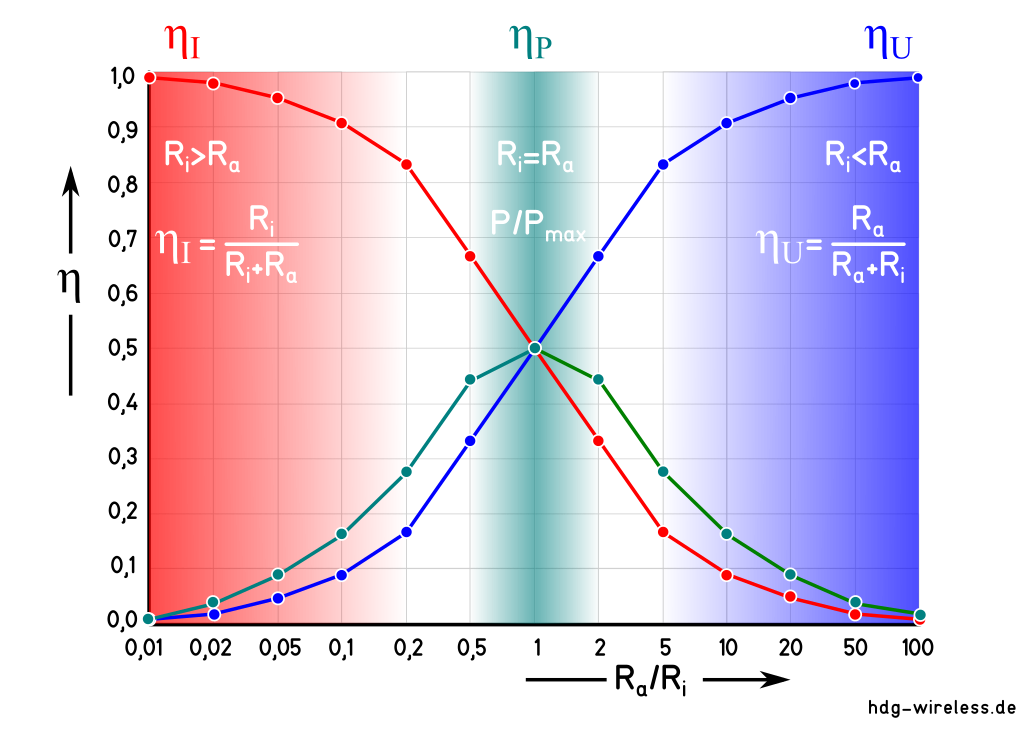
η = Wirkungsgrad [1]
I = Strom [A]
P = Leistung [W]
U = Spannung [V]
R_i = Quellwiderstand [Ω]
R_a = Lastwiderstand [Ω]

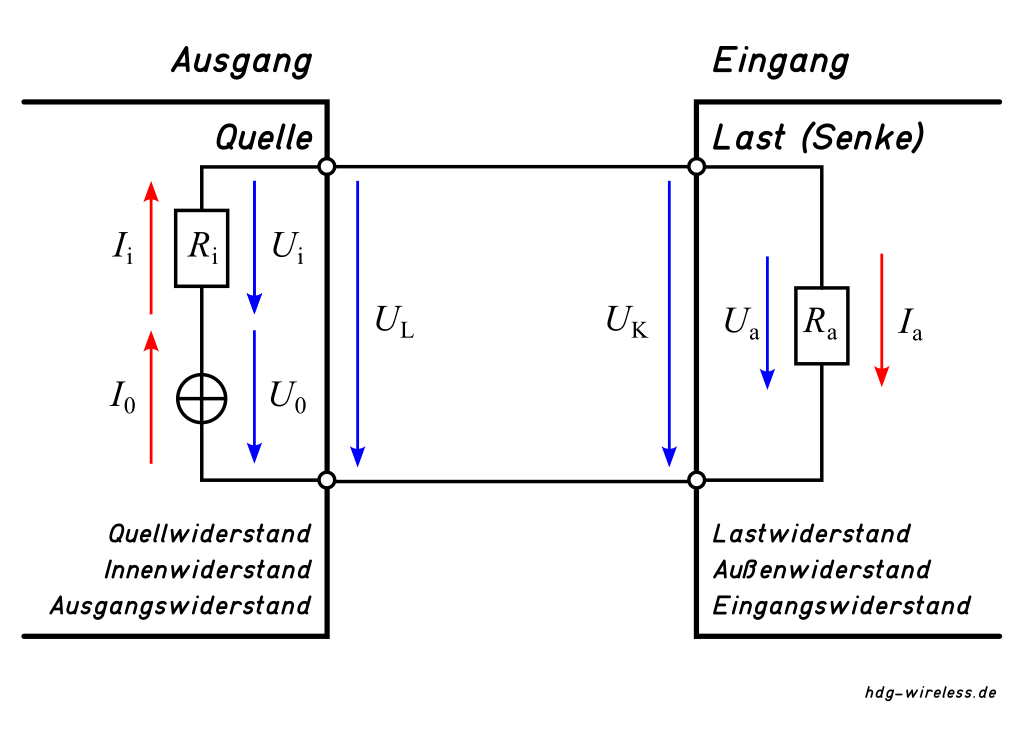
U₀ = Quellenspannung [V]
I₀ = Quellenstrom [A]
U_i = Spannungsabfall am Innenwiderstand [V]
U_a = Spannungsabfall am Außenwiderstand [V]
U_L = Leerlaufspannung [V]
U_K = Klemmenspannung [V]
I_i = Stromfluß durch den Innenwiderstand [A]
I_a = Stromfluss durch den Außenwiderstand [A]
R_i = Innenwiderstand [Ω]
R_a = Außenwiderstand [Ω]

Bei einer Signalquelle mit sinusförmigen Spannungs- oder Stromverlauf (Wechselspannung bzw. Wechselstrom) und der komplexen Innenimpedanz Z_i

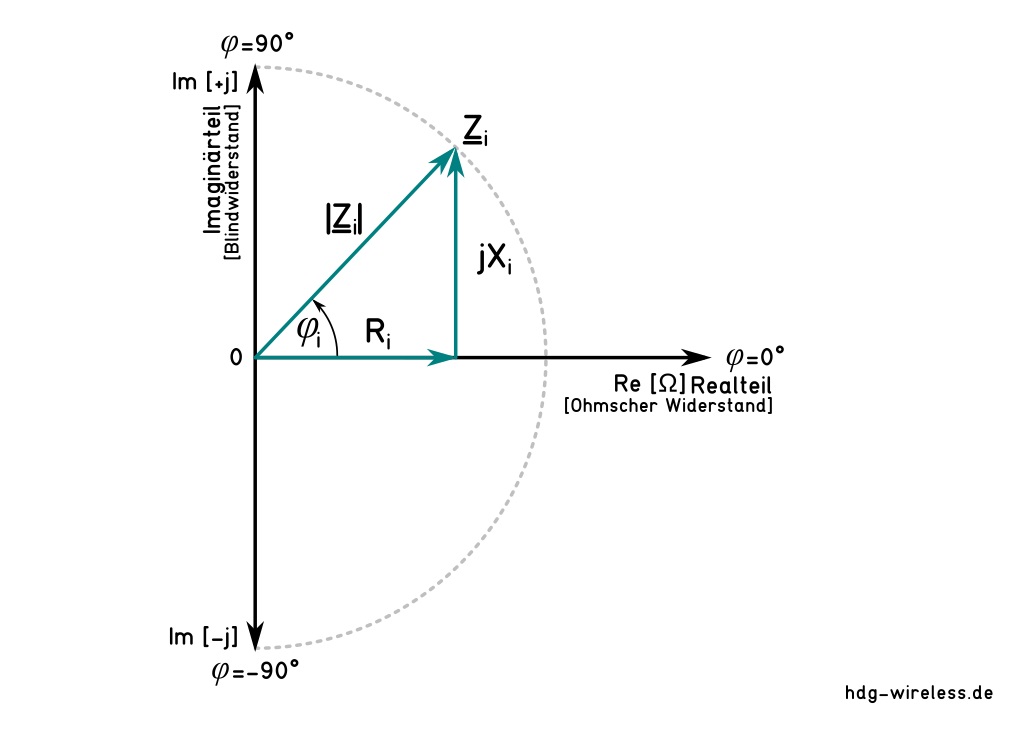
kann die maximale Leistung P nur dann entnommen werden, wenn die Außenimpedanz Z_a konjugiert komplex zur Innenimpedanz Z_i gewählt wird:

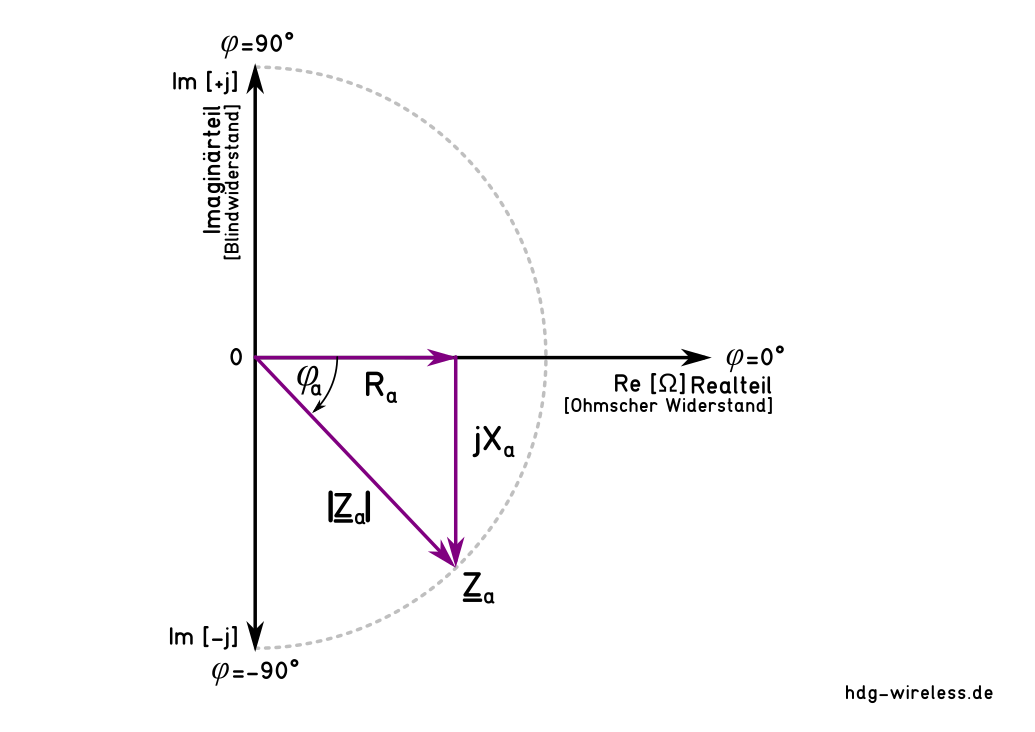
Diesen speziellen Fall sind die Realteile Re gleich groß (Innenwiderstand R_i = Außenwiderstand R_a) und die Imaginärteile Im kompensieren sich zu Null (jX_i + jX_a = 0).

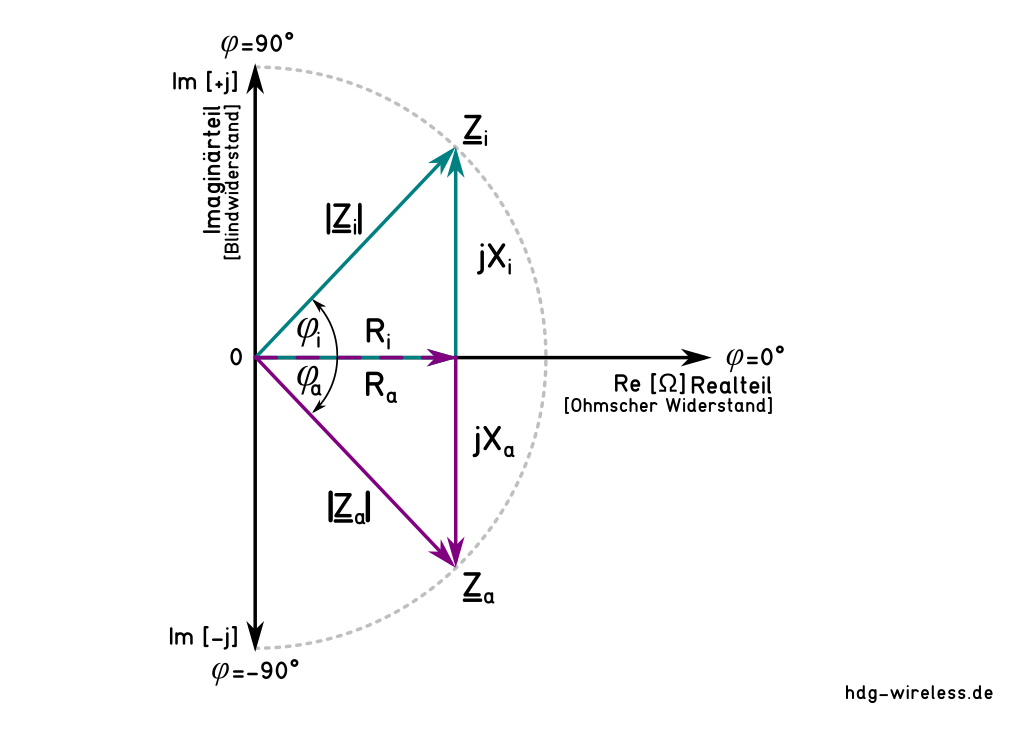
Dieser Zustand der komplexen Leistungsanpassung, bei dem sich die Blindwiderstände gegenseitig aufheben, bedingt sich ebenfalls aufhebende Phasenwinkel φ gleicher Weite (Winkelfeld W) und somit gleiche Kreisfrequenz ω, bzw. Frequenz f.

⇒ Anpassung
⇒ Impedanzanpassung
⇒ Quellwiderstand [ ⇒Innenwiderstand ]
⇒ Spannungsanpassung
⇒ Stromanpassung
⇒ Wirkungsgrad