Stehwellenverhältnis s
SWV, Standing-Wave-Ratio, SWR, Voltage Standing Wave Ratio, VSWR, Welligkeit, Welligkeitsfaktor
Das Stehwellenverhältnis s ist definiert als das Verhältnis von Spannungsmaximum Umax zu Spannungsminimum Umin.
Stehwellenverhältnis
(VSWR - voltage standing wave ratio):
s = Stehwellenverhältnis [1]
Umax = Spannungsmaximum [V]
Umin = Spannungsminimum [V]
Γ = Reflexionsfaktor [1]
Das Stehwellenverhältnis s ist ein Maß für die Anpassung einer Leitung an den Verbraucher und zeigt die Größe des reflektierten Anteils einer ausgesendeten Welle.
Das Stehwellenverhältnis s kann Werte zwischen 1 und ∞ annehmen.
| s = 1 | Anpassung | Umin = Umax |
| s = ∞ | Kurzschluß, bzw. Leerlauf | Umin = 0 |
Stehwellenverhältnis (Leistung P):
Das Stehwellenverhältnis s kann auch aus dem Verhältnis der hinlaufenden Leistung P↦ zur rücklaufenden Leistung P⇤ berechnet werden:
s = Stehwellenverhältnis [1]
P↦ = Leistung (hinlaufend) [W]
P⇤ = Leistung (rücklaufend) [W]
Stehwellenverhältnis (Reflexionsfaktor Γ):
Das Stehwellenverhältnis s kann auch aus dem Reflexionsfaktor Γ berechnet werden:
s = Stehwellenverhältnis [1]
Γ = Reflexionsfaktor [1]
Ra = ZL
Wird eine (theoretisch) verlustlose Leitung mit einem Lastwiderstand Ra abgeschlossen, der dem Leitungswellenwiderstand ZL entspricht (Ra = ZL), wird die gesamte Leistung P im Lastwiderstand Ra umgesetzt.
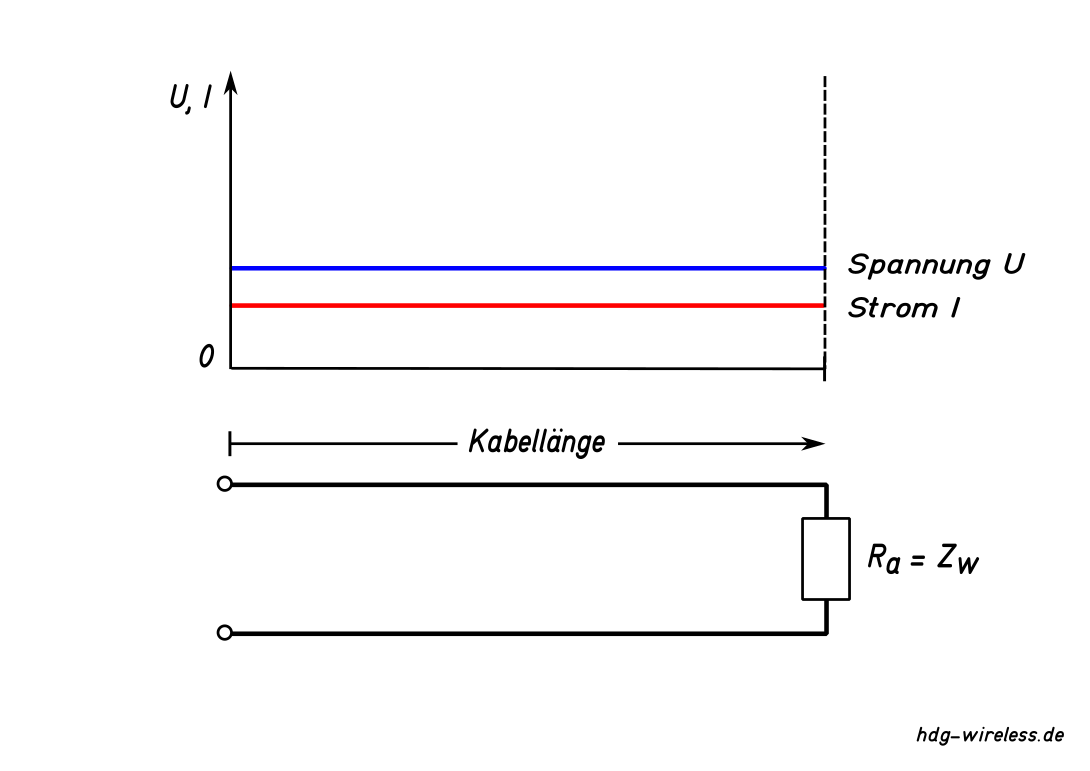
D.h. die Leistung P wird am Abschlußwiderstand vollständig verbraucht und es kommt zu keiner Reflexion. Die Spannung U (und auch der Strom I) ist an allen Punkten der Leitung in gleichbleibender Größe verteilt.
Ra ≠ ZL
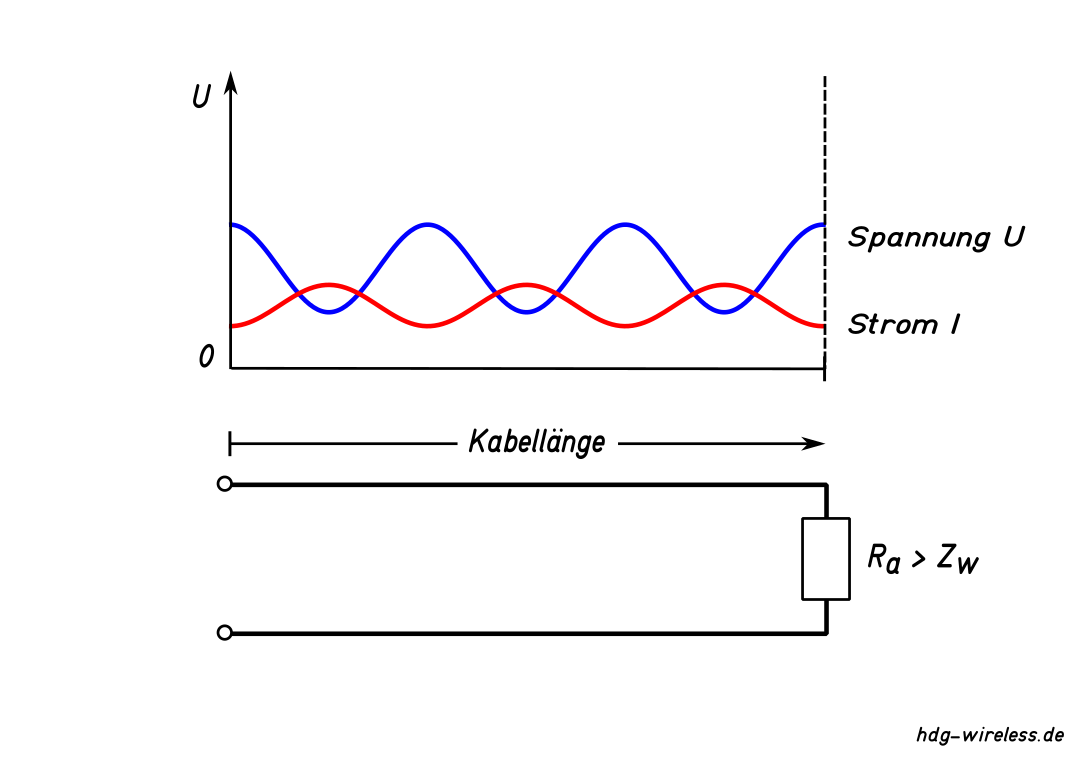
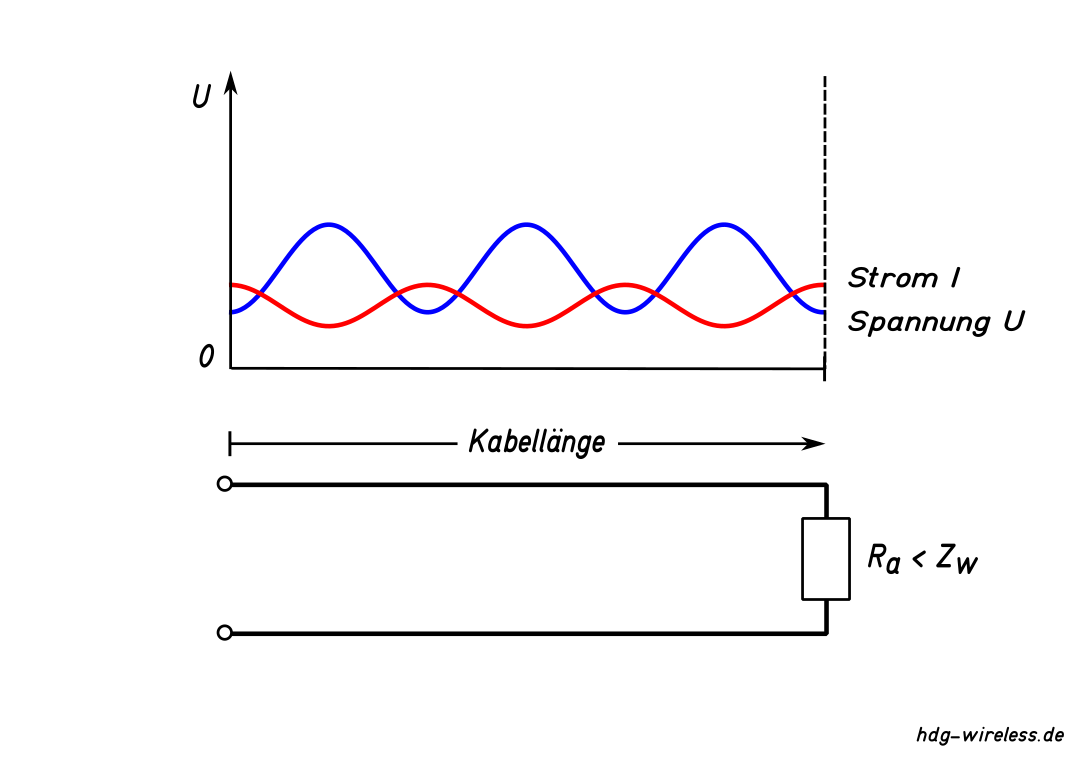
Ist der Leitungswellenwiderstand ZL nicht gleich dem Lastwiderstand Ra des Verbrauchers (z.B. Antenne), kommt es an der Schnittstelle zu einer Reflexion (Reflexionsfaktor Γ, Stehwellenverhältnis s) von Teilen der ankommenden Welle bis hin zur Totalreflexion.
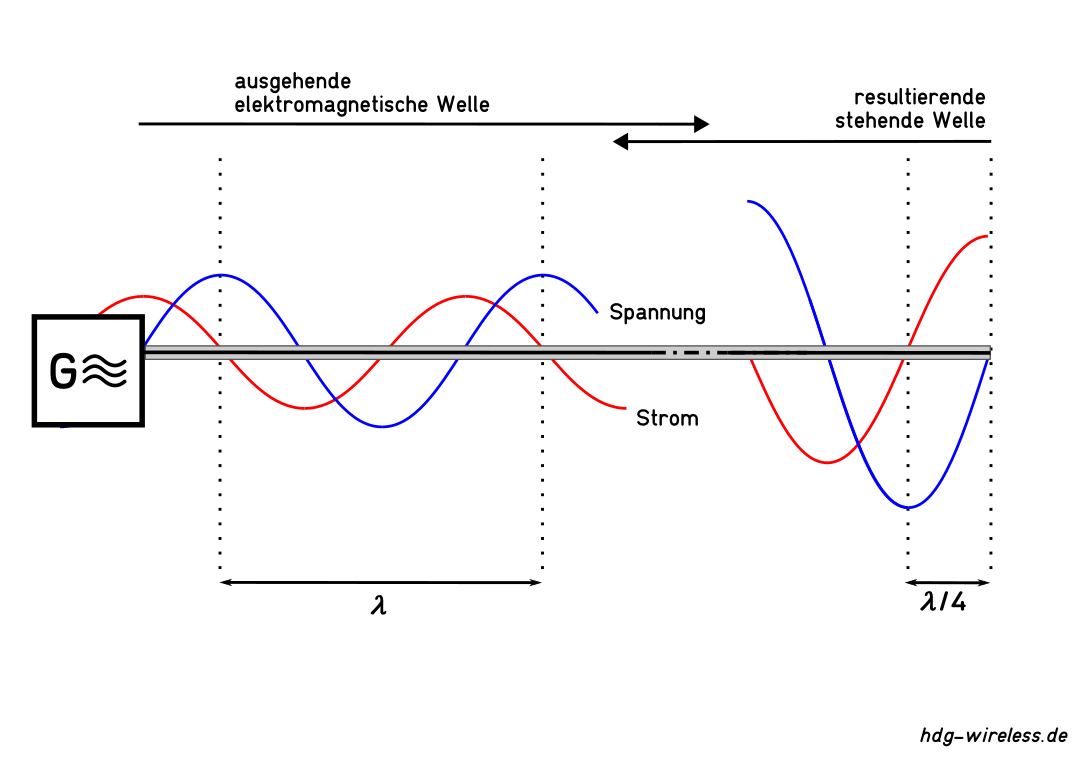
Die Überlagerung der beiden Wellen (z.B. der hinlaufenden Spannung U↦ mit der rücklaufenden Spannung U⇤) bildet entlang der Leitung eine stehende Welle, die örtlich konstante Minimal- & Maximalwerte von Strom I und Spannung U zeigt.
Leerlauf:
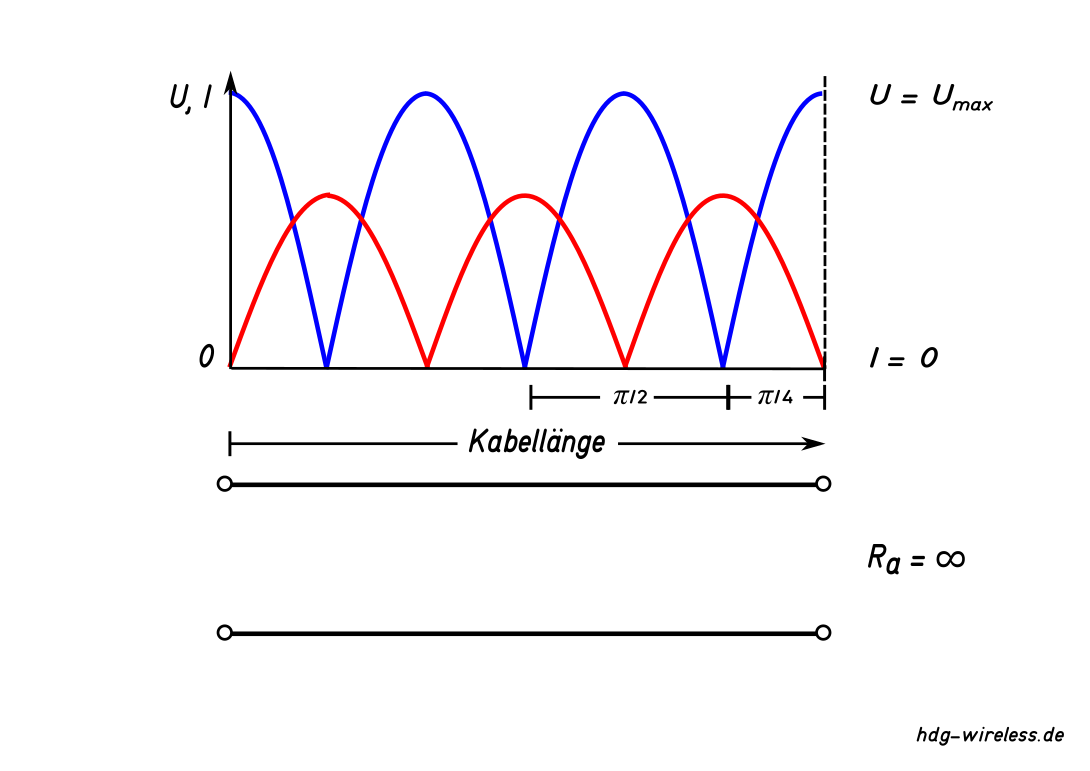
Leerlauf (Ra = ∞)
Wird der Lastwiderstand Ra (z.B. Antenne oder Abschlußwiderstand RT) einer Leitung entfernt, so stellt die offene Leitung für den Strom I einen unendlich großen Widerstand R dar (Ra = ∞) und es fließt kein Strom. Am Leitungsende befindet sich somit eine Stromnullstelle und es kommt zur Totalreflexion von Spannung U und Strom I.

Aufgrund der Laufzeit (Ausbreitungsgeschwindigkeit c x Verkürzungsfaktor VF(1/√εr)) von Strom I und Spannung U in der Leitung überlagern sich hin- und rücklaufende Welle zu einer stehenden Welle.
Über die Länge l der Speiseleitung verteilt finden sich im λ/4-Abstand Spannungsmaxima Umax und Spannungsminima Umin die am jeweiligen Ort die Vektorsumme der gegenläufigen Spannungen darstellen.
Spannung U und Strom I sind um 90° (λ/4) verschoben.
Einem Spannungsmaximum Umax steht somit ein Stromminimum Imin gegenüber und umgekehrt.
Durch den unendlich großen Lastwiderstand (Ra = ∞) ist am Leitungsende die Spannung U maximal und es liegt ein Spannungsbauch vor.
Der Strom I ist an dieser Stelle minimal und bildet eine Stromnullstelle aus.
Ein HF-Generator erzeugt im zeitlichen Verlauf der (Wechsel-) Spannung U Wellen unterschiedlicher Spannungswerte auf der angeschlossenen Leitung, sog. Wanderwellen.
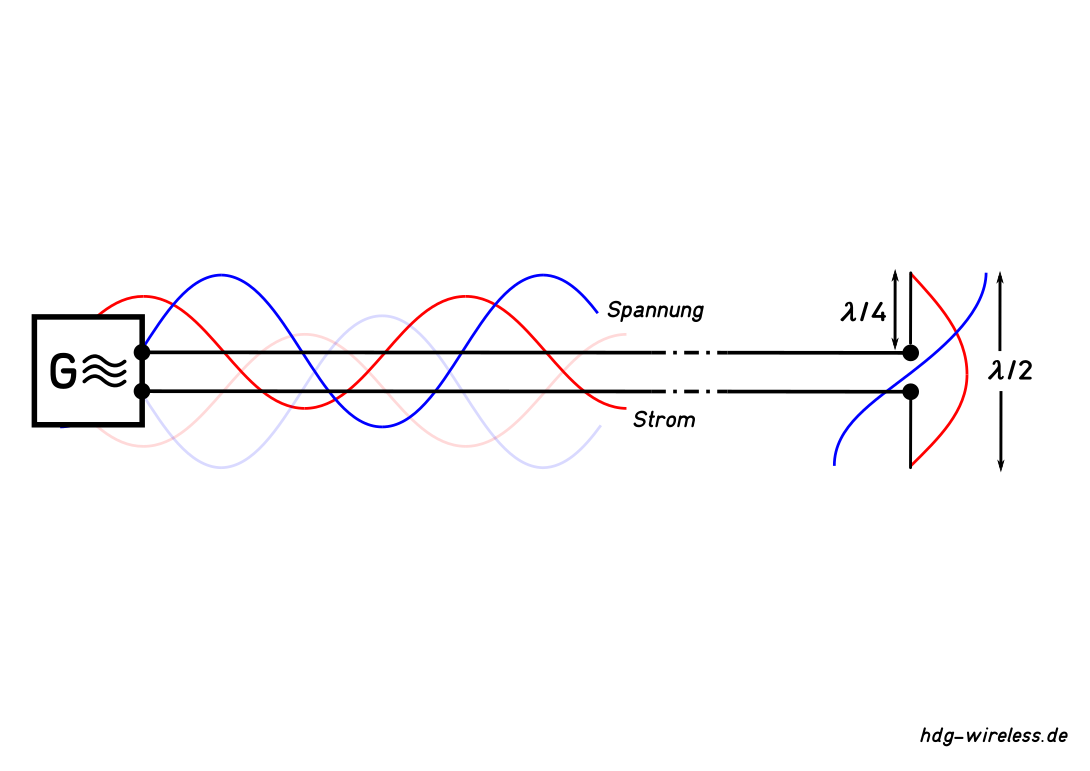
Die verschiedenen Spannungswerte von Spannungsminimum Umin bis Spannungsmaximum Umax wanderen in Ausbreitungsgeschwindigkeit c der Welle (bzw. Phasengeschwindigkeit vp) die Leitung entlang.
Kurzschluß (Ra = 0)
Ist eine Leitung kurzgeschlossen, also kein Lastwiderstand Ra (Ra = 0) vorhanden, wird der Strom I am "Leitungsende" maximal.
An der Kurzschluß-Stelle kann keine Spannung U aufgebaut werden und es kommt zu einer stehenden Welle, die in ihrer Verteilung von Spannung U und Strom I um die Wellenlänge λ/4 von der des Leerlaufs verschoben ist.
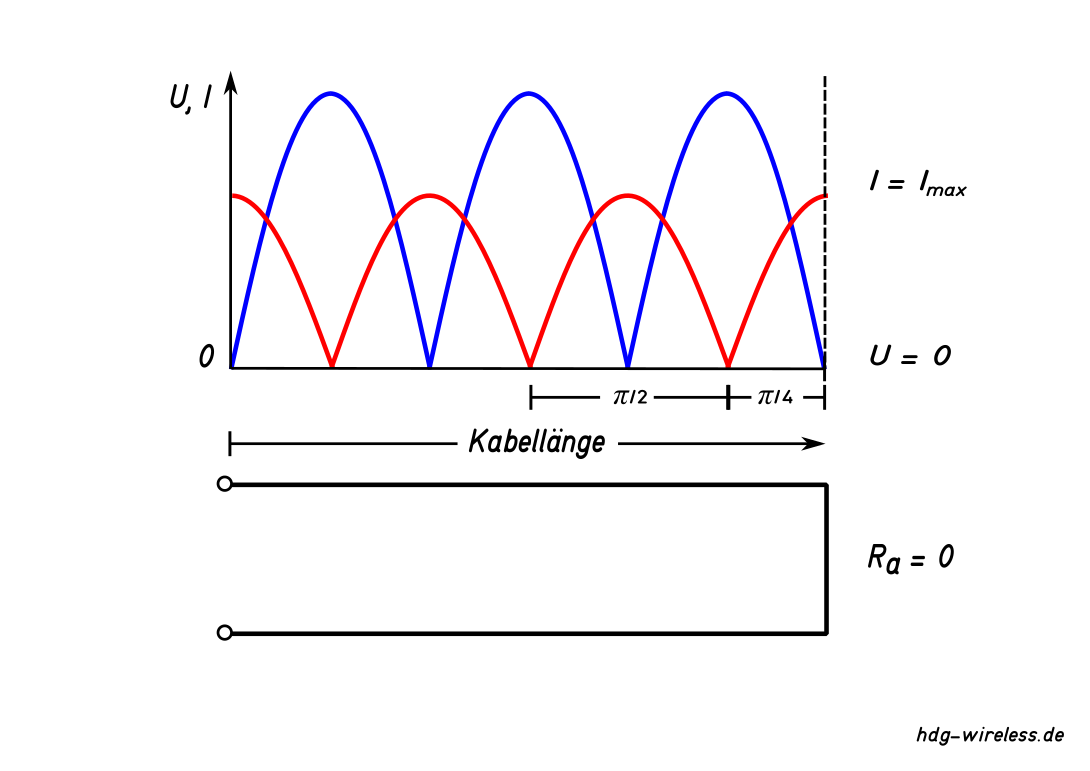
Auch in diesem Fall wird von Totalreflexion gesprochen und am Leitungsende befinden sich ein Strombauch und eine Spannungsnullstelle.
Demnach steht auch hier einem Spannungsmaximum Umax ein Stromminimum Imin gegenüber. Spannung U und Strom I sind um 90° (λ/4) verschoben.
Reflexionsfaktor Γ ⇄ Rückflussdämpfungsfaktor RL ⇄ Stehwellenverhältnis s
Reflexionsfaktor Γ:
Der Reflexionsfaktor Γ (≙ Reflexionskoeffizient r ) ist definiert als das Verhältnis aus rücklaufender Spannung U⇤ zur hinlaufenden Spannung U↦.
Γ = Reflexionsfaktor [1]
U⇤ = Spannung (rücklaufend) [V]
U↦ = Spannung (hinlaufend) [V]
I⇤ = Strom (rücklaufend) [A]
I↦ = Strom (hinlaufend) [A]
P⇤ = Leistung (rücklaufend) [W]
P↦ = Leistung (hinlaufend) [W]
ZV = Lastimpedanz [Ω]
ZW = Wellenwiderstand (1,2 vor/nach der Schnittstelle) [Ω]
s = Stehwellenverhältnis [1]

Rückflussdämpfungsfaktor RL:
Der Rückflussdämpfungsfaktor RL beschreibt das Verhältnis von hinlaufender Leistung P↦ zu rücklaufender Leistung P⇤ in einem Antennenkabel oder HF-System.
RL = Rückflussdämpfungsfaktor (Return Loss) [1]
P↦ = Leistung "hinlaufend" [W]
P⇤ = Leistung "rücklaufend" [W]
U↦ = Spannung (hinlaufend) [V]
U⇤ = Spannung (rücklaufend) [V]
Γ = Reflexionsfaktor [1]

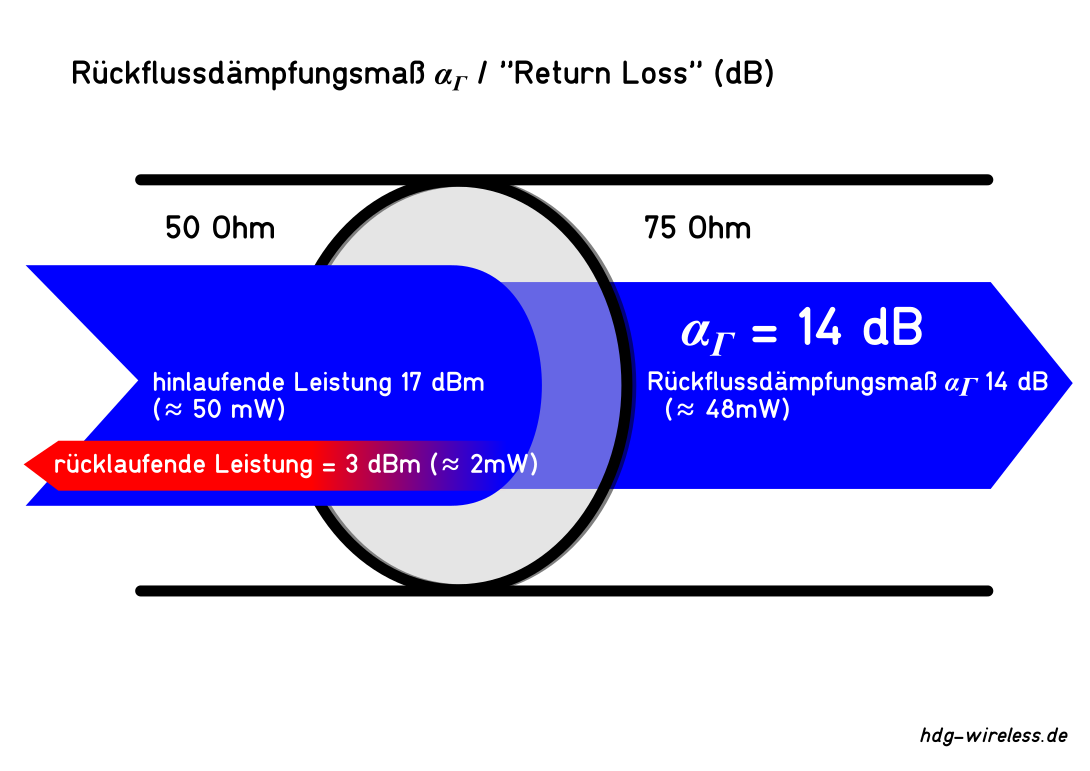
Rückflussdämpfungsmaß αΓ:
Das Rückflussdämpfungsmaß αΓ ist der logarithmierte Rückflussdämpfungsfaktor RL und beschreibt das Verhältnis von hinlaufender Leistung P↦ zur rücklaufenden Leistung P⇤ in einem Antennenkabel.
αΓ = Rückflussdämpfungsmaß [dB]
P↦ = hinlaufende Leistung [W]
P⇤ = rücklaufende Leistung [W]
RL = Rückflussdämpfungsfaktor (Return Loss) [1]
Γ = Reflexionsfaktor [1]
Stehwellenverhältnis s:
Das Stehwellenverhältnis s ist definiert als das Verhältnis von Spannungsmaximum Umax zu Spannungsminimum Umin.
s = Stehwellenverhältnis [1]
Umax = Spannungsmaximum [V]
Umin = Spannungsminimum [V]
Γ = Reflexionsfaktor [1]

Formelsammlung
⇒ Leitungswellenwiderstand
⇒ Wellenlänge
⇒ Wellenwiderstand
⇒ Widerstand