Anpassungstransformator
Impedanzwandler
Der Begriff Anpassungstransformator ist in der HF-Technik nicht definiert, wird aber umgangssprachlich meist synonym für Impedanzwandler verwendet.
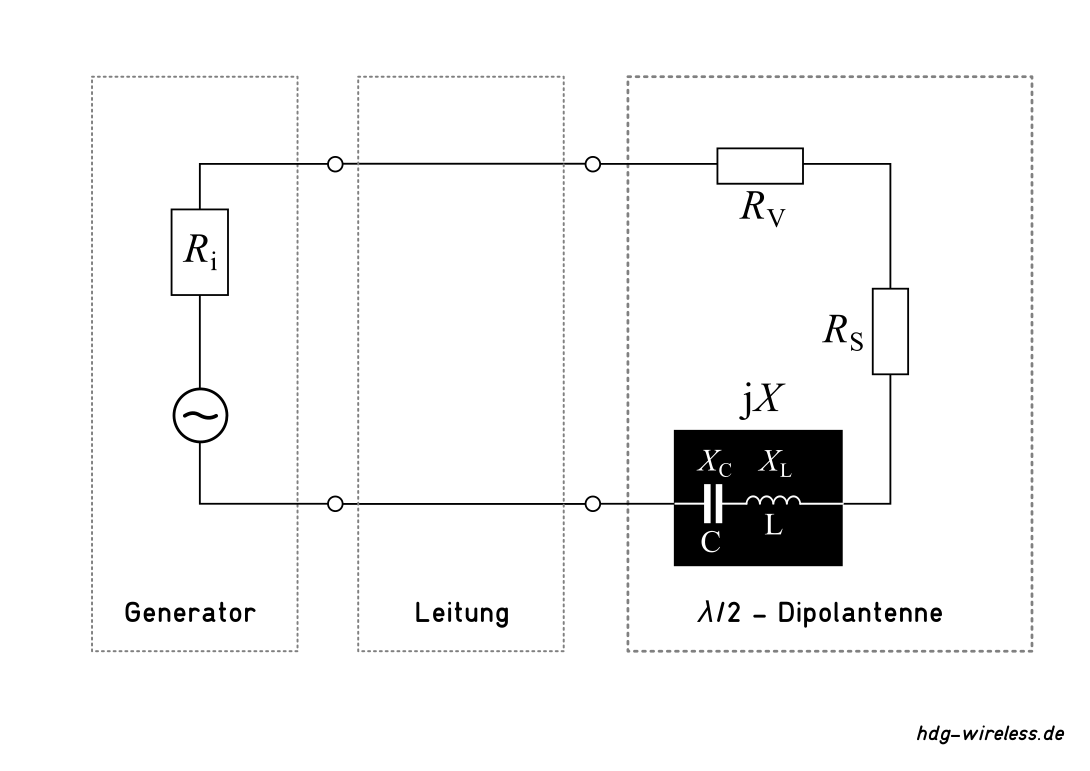
Verwirrend ist, dass im Grunde nur der (Teil-)Begriff der Anpassung gemeint ist, d.h. sowohl die elektrische Widerstandsanpassung (i.e.S. die Leistungsanpassung Ri = Ra) als auch die Wellenwiderstandsanpassung der Leitungswellenwiderstände ZL (zwischen Senderausgang, Speiseleitung und Antenneneingang) gemeint sein kann [1].
"Gewandelt" oder "transformiert", z.B. im Sinne der Spannungswandlung durch Induktion der Spulen eines Transformators, wird bei Leistungsanpassung Ri = Ra und der Anpassung der Leitungswellenwiderstände ZL nicht.
[1] Hinzu kommt die falsche Verwendung des Begriffs für die Symmetrierung einer unsymmetrischen Koaxialleitung an eine symmetrische Dipolantenne oder die vermeintliche Anpassung des Leitungswellenwiderstands ZL an den Freiraumwellenwiderstand Z0.
Um den umgangssprachlich verwirrenden Begriff des Anpassungstransformators etwas zu entwirren zunächst die Defintion der Anpassung:
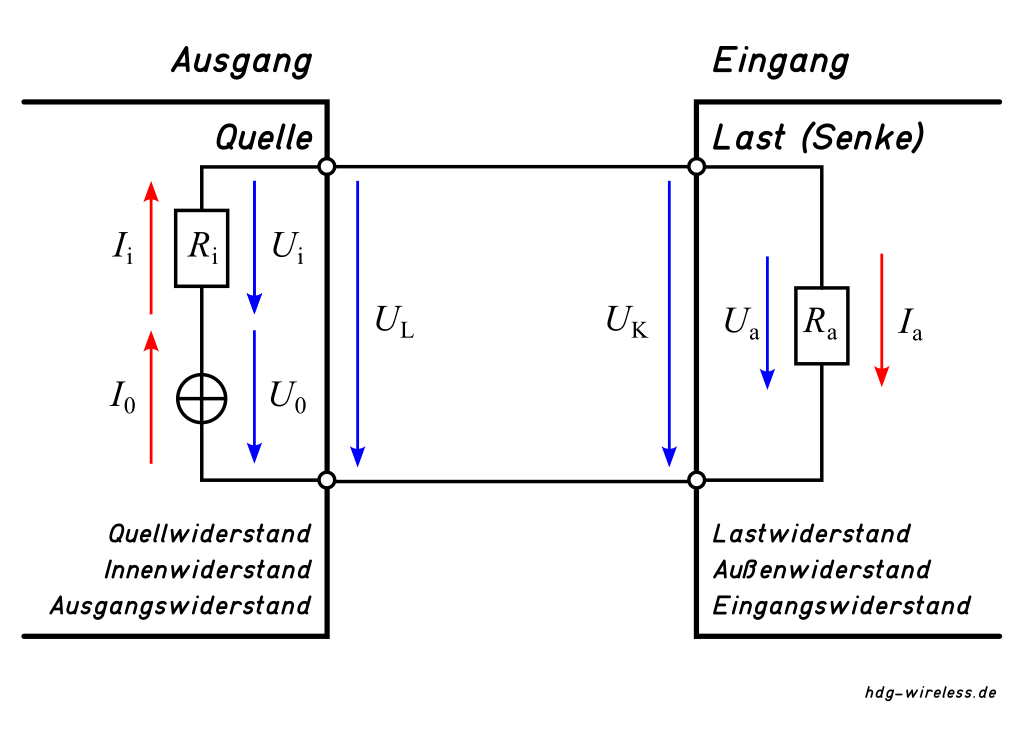
Bei der Anpassung zwischen elektrischen Baugruppen handelt es sich um elektrische Anpassungsschaltungen, i.d.R. Widerstandsanpassungen zwischen Quellwiderstand Ri und Lastwiderstand Ra, die einen maximalen Wirkungsgrad η der Schaltung zwischen Signal-Quelle und Signal-Empfänger erzielen sollen.
Dabei ist die Leistungsanpassung Ri = Ra die in der HF-Technik vorherrschende Anpassungsform:
Die Leistungsanpassung Ri = Ra ist eine Widerstandsanpassung, bei der Quellwiderstand Ri und Lastwiderstand Ra den gleichen Wert haben.
Leistungsanpassung: Ri = Ra [Zi = Za]
Dabei handelt es sich um eine elektrische Anpassungsschaltung, die einen maximalen Wirkungsgrad η erzielen soll.
Um es konkret in Zahlen auszusprechen: In einem 50-Ohm-System müssen der Innenwiderstand Ri des Senders, genauso wie der Außenwiderstand Ra der Antenne, 50 Ohm aufweisen, d.h. ein rein ohmscher Widerstand R wird als 50-Ohm-Abschlußwiderstand RT antselle der Antenne die Leistung P des Senders zur Hälfte in Wärme umwandeln. Die andere Hälfte wird bei Leistungsanpassung Ri = Ra bereits im Innenwiderstand Ri in Wärme umgesetzt.
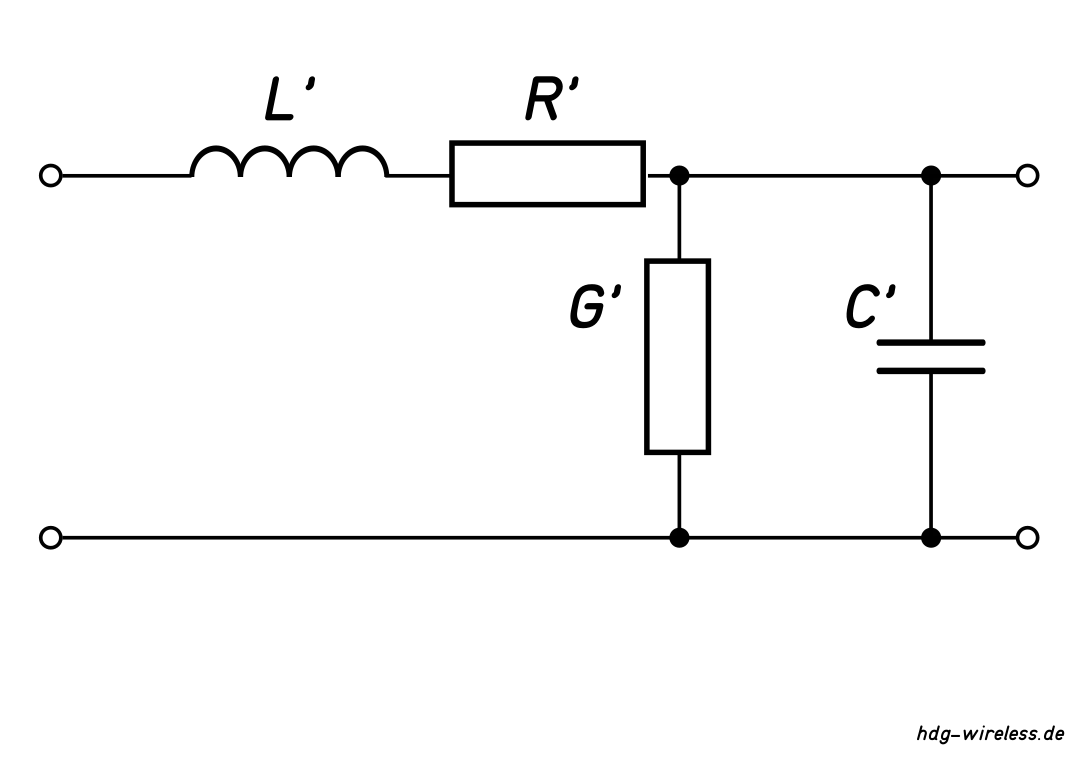
Der Leitungswellenwiderstand ZL ist definiert:
Der Leitungswellenwiderstand ZL ist eine Eigenschaft längshomogener Leitungen und beschreibt den Wellenwiderstand ZW, welcher der Ausbreitung elektromagnetischer Wellen in einer elektrischen Leitung entgegenwirkt.
Der Leitungswellenwiderstand ZL muss in diesem 50-Ohm-System ebenfalls 50 Ohm aufweisen, darf aber nicht wie ein 50-Ohm-Abschlußwiderstand RT die Leistung P in Wärme umwandeln, sondern sollte im theoretischen Idealfall keinen ohmschen Widerstand R darstellen.
Anhand der Formel wird deutlich, dass in diesem Idealfall lediglich das Verhältnis von Induktivitätsbelag L' zum Kapazitätsbelag C' für den Leitungswellenwiderstand ZL von 50 Ohm verantwortlich sind (L' = 2500·C').
ZL(Koax) = Leitungswellenwiderstand Koaxialkabel [Ω]
L' = Induktivitätsbelag [Hm-1]
C' = Kapazitätsbelag [Fm-1]
R' = Widerstandsbelag [Ωm-1]
G' = Ableitungsbelag [Sm-1]
j = imaginäre Einheit [1]
ω = Kreisfrequenz [s-1]
π = Kreiszahl (Pi) [1]
Z0 = Freiraumwellenwiderstand [Ω]
εr = Relative Permittivität [1]
D = Aussendurchmesser [m]
d = Innendurchmesser [m]
Das Verhältnis Induktivitätsbelag L' zu Kapazitätsbelag C' hat wiederum direkten Einfluß auf die Kabelgeometrie, da je dünner die Leiter desto größer die Induktivität L und je größer der Abstand der Leiter zueinander desto kleiner ist die Kapazität C.
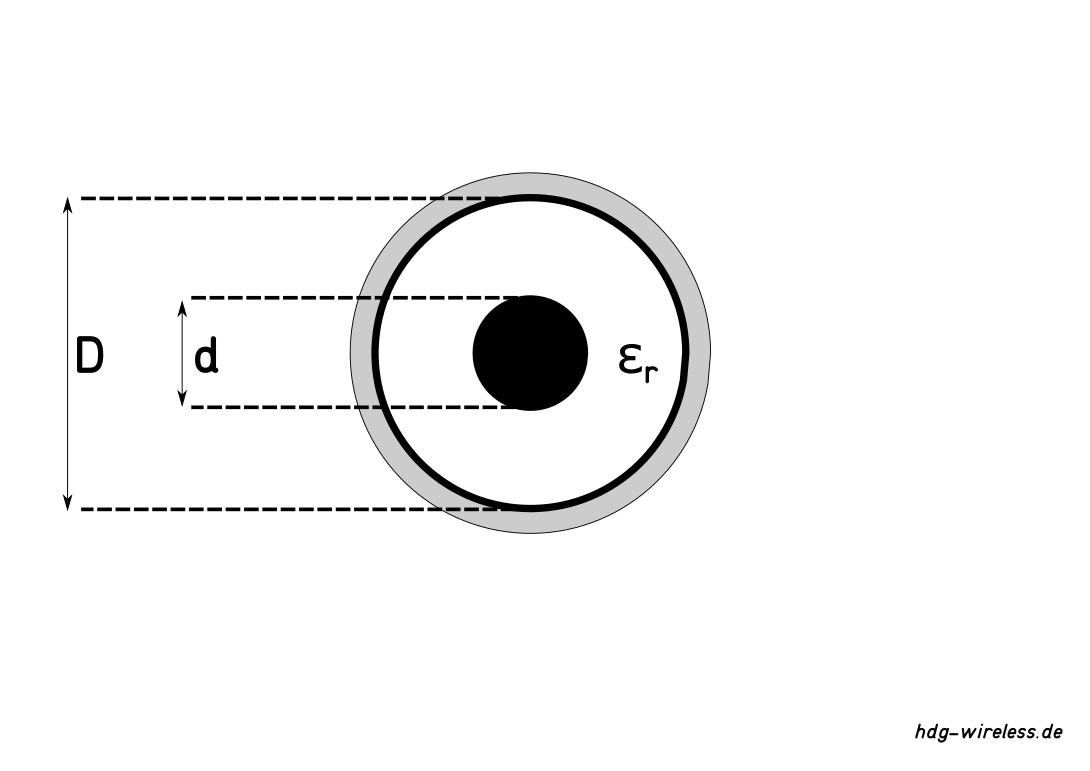
Die Induktivität L und Kapazität C sind ebenfalls abhängig von der relativen Permittivität εr des dazwischen liegenden Dielektrikums.
Für Luft (εr = 1) als Dielektrikum ergibt das ein Verhältnis von Aussendurchmesser D zu Innendurchmesser d von D = 2,3d.
|
Koaxialkabel ∅: D5mm/d für 50 Ω & 75 Ω Permitivitätswert Dielektrikum:Luft: εr = 1 |
|||
| d | D | εr | ZW |
|---|---|---|---|
| 2,17 mm | 5 mm | 1,0 | 50 Ω |
| 1,43 mm | 5 mm | 1,0 | 75 Ω |