Leitungswellenwiderstand ZL
Kabelimpedanz, Kennwiderstand, Nennimpedanz
Der Leitungswellenwiderstand ZL ist eine Eigenschaft längshomogener Leitungen und beschreibt den Wellenwiderstand ZW, welcher der Ausbreitung elektromagnetischer Wellen in einer elektrischen Leitung entgegenwirkt.
Leitungswellenwiderstand:
ZL(Koax) = Leitungswellenwiderstand Koaxialkabel [Ω]
L' = Induktivitätsbelag [Hm-1]
C' = Kapazitätsbelag [Fm-1]
R' = Widerstandsbelag [Ωm-1]
G' = Ableitungsbelag [Sm-1]
j = imaginäre Einheit [1]
ω = Kreisfrequenz [s-1]
π = Kreiszahl (Pi) [1]
Z0 = Freiraumwellenwiderstand [Ω]
εr = Relative Permittivität [1]
D = Aussendurchmesser [m]
d = Innendurchmesser [m]
Der Leitungswellenwiderstand ZL ist eine charakteristische Kenngröße längshomogener Leitungen und wird benötigt, um den realen Widerstandswert (ohmscher Widerstand R) zu ermitteln, mit dem eine Leitung abgeschlossen werden muss, damit Anpassung vorliegt und Reflexionen der übertragenen Signale im Kabel verhindert werden.
Der Leitungswellenwiderstand ZL läßt sich aus dem Kapazitätsbelag C' und dem Induktivitätsbelag L' berechnen.
ZL = Leitungswellenwiderstand [Ω]
L' = Induktivitätsbelag [Hm-1]
C' = Kapazitätsbelag [Fm-1]
Ein Antennenkabel (Speiseleitung) kann als fortlaufende Kombination von Parallelkapazitäten C und Reiheninduktivitäten L beschrieben werden.
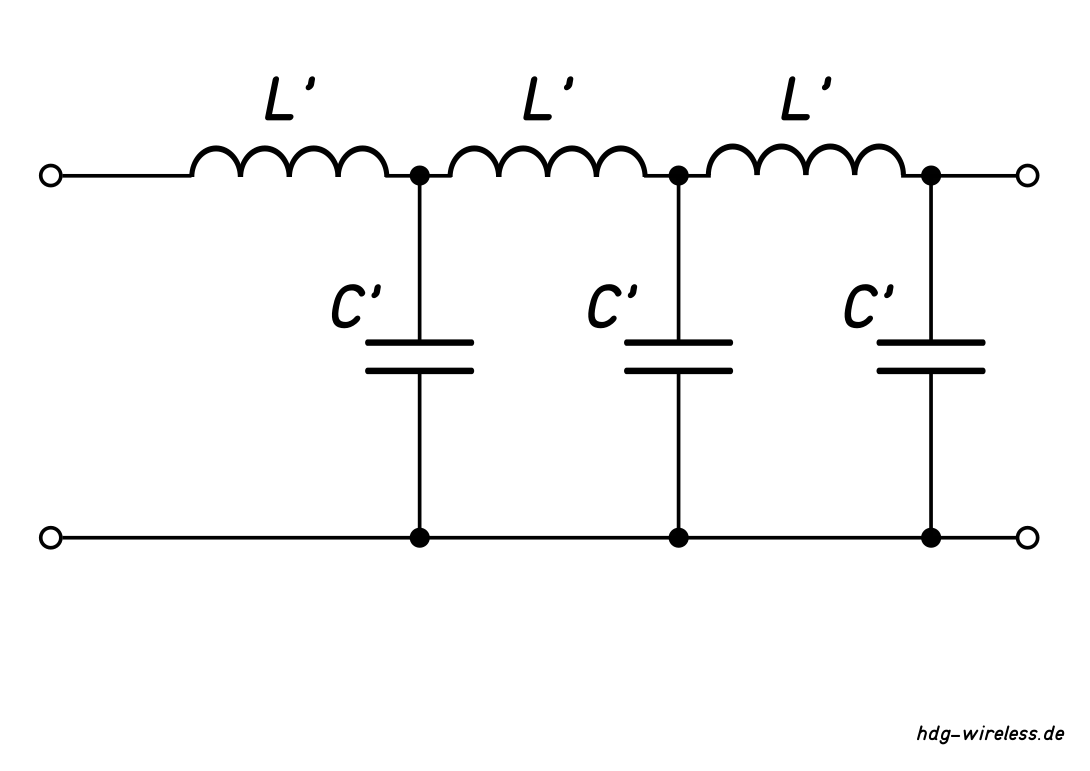
In der Länge des Leiters steckt die Induktivität L, d.h. der gestreckte Leiter wird als eine abgewickelte Spule betrachtet.
Der Leitungswellenwiderstand ZL wird vom mechanischen Aufbau des Kabels und der relativen Permittivität εr des Dielektrikums bestimmt.
ZL(Koax) = Leitungswellenwiderstand Koaxialkabel [Ω]
Z0 = Freiraumwellenwiderstand [Ω]
π = Kreiszahl (Pi) [1]
εr = Relative Permittivität [1]
D = Durchmesser (Aussenleiter Koaxialkabel) [m]
d = Durchmesser (Innenleiter Koaxialkabel) [m]
Bei einer (theoretisch) unendlichen Leitung ergibt sich ein charakteristischer Leitungswellenwiderstand ZL der betrachteten Leitungsbeläge (bzw. Kabelgeometrie), mit dem ein reales Kabel abgeschlossen werden muss, damit eine Anpassung hergestellt ist und Verluste durch Fehlanpassung vermieden werden können.
Der Leitungswellenwiderstand ZL ist an jedem Punkt auf einer Leitung über das Verhältnis vom Strom I zur Spannung U verknüpft.
ZL = Leitungswellenwiderstand [Ω]
U = Spannung [V]
I = Strom [A]
Der Wellenwiderstand ZW ist theoretisch[1] unabhängig von der Frequenz und von der Länge der Leitung.
[1] Die Frequenzunabhängigkeit gilt nur bei unversehrten Leitungen, also Leitungen, deren Leitungsgeometrie nicht durch Knicke und Quetschungen verändert ist.
Die in einem Kabel übertragene Leistung P ist bei Leistungsanpassung Ri = Ra:
P = Leistung [W]
U = Spannung [V]
I = Strom [A]
ZL = Leitungswellenwiderstand [Ω]
Definition des Wellenwiderstandes ZW einer Koaxialleitung:
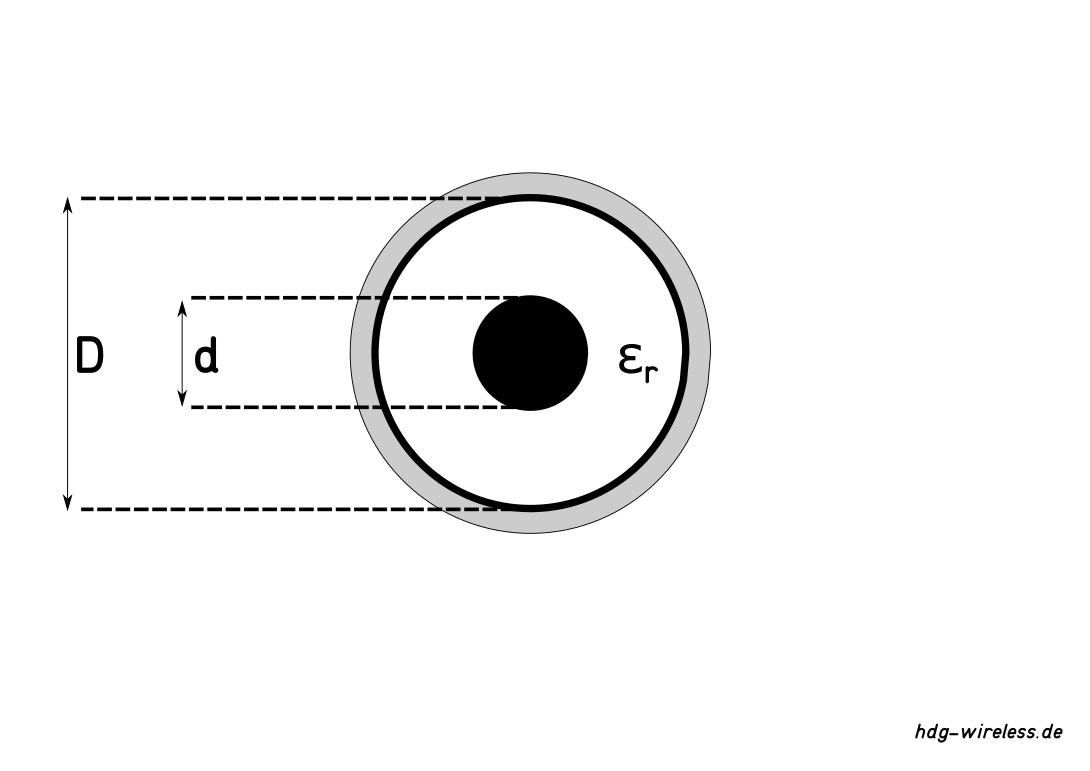
Der mechanische Aufbau des Kabels und die relative Permittivität εr des Dielektrikums bestimmen den Leitungswellenwiderstand ZL.
Dabei wird die Impedanz Z u.a. durch das Verhältnis der Durchmesser von Innen- zu Außenleiter ermittelt.[1]
ZL(Koax) = Leitungswellenwiderstand Koaxialkabel [Ω]
εr = Relative Permittivität [1]
D = Durchmesser (Aussenleiter Koaxialkabel) [m]
d = Durchmesser (Innenleiter Koaxialkabel) [m]
für (ZL = 50 Ω, εr = 1)
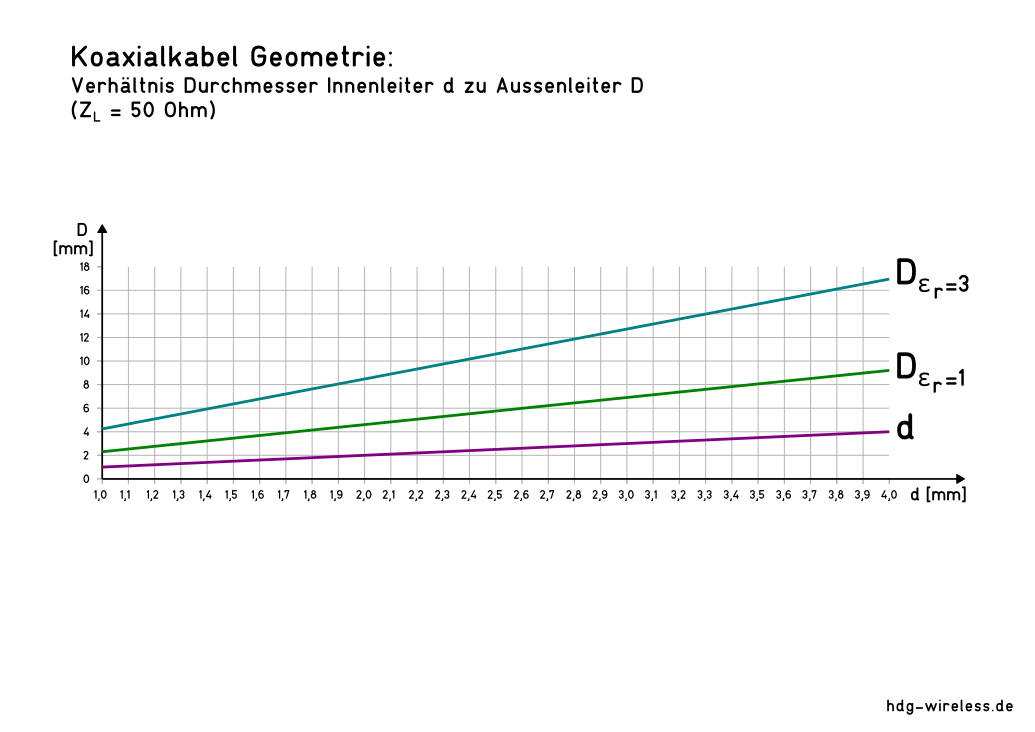
|
Koaxialkabel ∅: D5mm/d für 50 Ω & 75 Ω  Permitivitätswert Dielektrikum:
Permitivitätswert Dielektrikum:Polyethylen: εr = 2,3 |
|||
| d | D | εr | ZW |
|---|---|---|---|
| 2,17 mm | 5 mm | 1,0 | 50 Ω |
| 1,80 mm | 5 mm | 1,5 | 50 Ω |
| 1,54 mm | 5 mm | 2,0 | 50 Ω |
| 1,34 mm | 5 mm | 2,5 | 50 Ω |
| 1,43 mm | 5 mm | 1,0 | 75 Ω |
| 1,08 mm | 5 mm | 1,5 | 75 Ω |
| 0,85 mm | 5 mm | 2,0 | 75 Ω |
| 0,69 mm | 5 mm | 2,5 | 75 Ω |
|
Koaxialkabel ∅: D10mm/d für 50 Ω & 75 Ω  Permitivitätswert Dielektrikum:
Permitivitätswert Dielektrikum:Polyethylen: εr = 2,3 |
|||
| d | D | εr | ZW |
|---|---|---|---|
| 4,34 mm | 10 mm | 1,0 | 50 Ω |
| 3,60 mm | 10 mm | 1,5 | 50 Ω |
| 3,07 mm | 10 mm | 2,0 | 50 Ω |
| 2,68 mm | 10 mm | 2,5 | 50 Ω |
| 2,86 mm | 10 mm | 1,0 | 75 Ω |
| 2,16 mm | 10 mm | 1,5 | 75 Ω |
| 1,71 mm | 10 mm | 2,0 | 75 Ω |
| 1,38 mm | 10 mm | 2,5 | 75 Ω |
Der Impedanzwert des Leitungswellenwiderstands ZL kann sich durch mechanische Einwirkung (zu kleine Biegeradien, Deformierung des Dielektrikums) verändern.
Eine Veränderung der Leitungsgeometrie durch mechanische Veränderung kann zu einer Änderung der Leitungsbeläge führen.
Ersatzschaltbild: Wellenwiderstandsbeläge
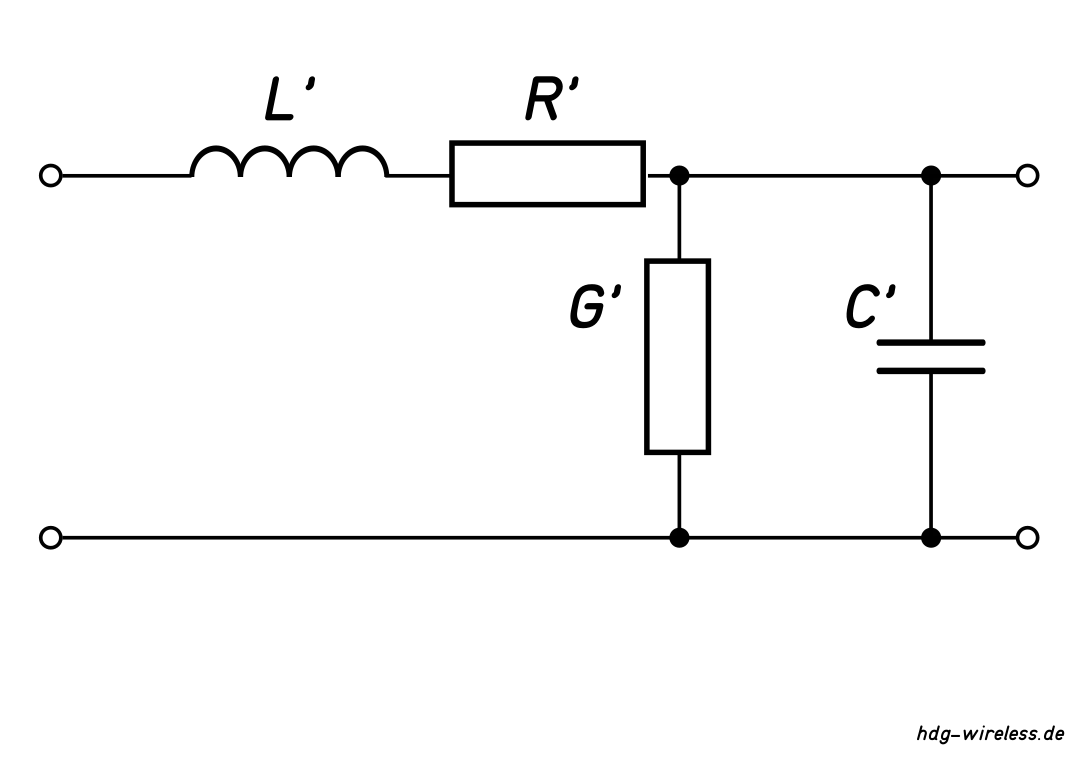
L' = Induktivitätsbelag [Hm-1]
R' = Widerstandsbelag [Ωm-1]
G' = Ableitungsbelag [Sm-1]
C' = Kapazitätsbelag [Fm-1]
Der Induktivitätsbelag L' und der Kapazitätsbelag C' sind abhängig von der Länge l der Leitung und der Frequenz f des Signals.
Bei lange Leitungen oder hohen Frequenzen haben sie einen großen Einfluß auf das Leitungsverhalten.
Für kurze Leitungen und niedrige Frequenzen sind sie eher vernachlässigbar.
Der Widerstandsbelag R' ist natürlich auch längenabhängig, die Betonung liegt hier aber auf der Frequenzabhängigkeit und somit auf der Kapazität C und Induktivität L.
?> und Induktivität L.
⇒ Anpassung
⇒ Antennenkabel
⇒ C-Belag [ ⇒Kapazitätsbelag ]
⇒ Dämpfung
⇒ Dielektrikum
⇒ Elektromagnetische Welle
⇒ Feldwellenwiderstand
Formelsammlung
⇒ Freiraumwellenwiderstand
⇒ Impedanz
⇒ Koaxialkabel
⇒ Kreiszahl
⇒ L-Belag [ ⇒Induktivitätsbelag ]
⇒ Leitungsbeläge
⇒ Relative Permittivität
⇒ Wellenwiderstand
⇒ Wellenwiderstand des Vakuums [ ⇒Freiraumwellenwiderstand ]
⇒ Widerstand